计算机组成原理笔记(一)
一、计算机系统概述
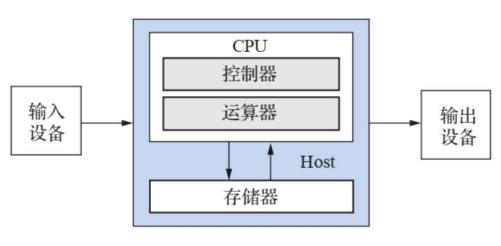
1.冯诺依曼体系结构
由运算器、控制器、存储器、输入设备和输出设备五部分组成
图解如下:
2. 计算机系统的组成
- 硬件系统组成
- 存储器:存放程序和数据(以二进制形式存放),按地址访问;
- 运算器:执行算术运算和逻辑运算;
- 控制器:根据指令的操作码、指令执行过程中的条件状态、时序系统等三方面的因素来产生指令执行过程中所需要的控制信号,控制数据的存取和程序的执行;
- 输入设备:将信息输入到计算机的外部设备,如键盘、鼠标等;
- 输出设备:输出计算机处理结果的外部设备。如显示器、打印机等。
- 软件系统组成
- 应用软件:解决应用问题的程序集合,如数据处理程序、情报检索程序等;
- 系统软件:管理和调度计算机,以方便用户使用计算机并提高计算机使用效率的程序的集合,包括:
- 操作系统
- 程序设计语言处理程序:编译器,汇编器,解释器
- 数据库管理系统
3.计算机的性能指标
(1)基本性能指标
- 字长:$ CPU $一次处理的数据位数,一般与计算机内部寄存器、运算器、数据总线的位宽相等,影响计算精确度和数据的表示范围与精度;
- 主存容量:主存能存储的最大信息量,由$ \underline{M\times N} $表示,其中$ M $表示字容量(存储单元数),$ N $表示位容量(每个存储单元的二进制位数)。
(2)与时间有关的性能指标
时钟周期:时钟频率(主频)的导数,是计算机处理操作最基本的时间单位;
- $ CPI $:执行每条指令所需的平均时钟周期数;
约定$ IC $表示所有指令的总条数,$ m $表示程序执行所需时钟周期数,$ P_{i} $表示某类指令的使用频率,$ IC_{i} $表示某类指令的条数,则满足$ CPI=\frac{m}{IC}=\sum\limits_{i=1}^{n}(CPI_{i}\times P_{i})=\sum\limits_{i=1}^{n}(CPI_{i}\times \frac{IC_{i}}{IC}). $
- $ IPC $:每个时钟周期$ CPU $能执行的指令条数;
$ IPC $满足:$ IPC=\frac{1}{CPI}. $
- $ CPU $时间:程序执行期间真正消耗$ CPU $的时间(包括用户$ CPU $时间和系统$ CPU $时间);
约定$ T $表示时钟周期时长,$ f $表示$ CPU $主频,则某段程序$ CPU $时间可表示为$ T_{cpu}=m\times T=\frac{m}{f}=CPI\times IC\times T=\frac{CPI\times IC}{f}. $
- $ MIPS $:每秒钟执行的百万条指令数;
约定$ f'=f\times 10^{6} $,则$ MIPS=\frac{IC}{T_{cpu}\times 10^{6}}=\frac{f}{CPI\times 10^{6}}=IPC\times f'. $
- $ MFLOPS $:每秒钟执行的浮点运算次数。
4.计算机系统的层次结构

二、数据信息的表示
1.数值数据的表示
(1)数值与机器码
- 数据格式是指使用二进制编码表示实际数据的结构形式,分类如下:
| 分类依据 | 具体分类 |
|---|---|
| 是否有符号位 | 无符号数和有符号数 |
| 小数点位置 | 定点数和浮点数 |
定点数和浮点数比较如下:
- 定点数:包括定点整数和定点小数
- 定点小数:小数点位置在最高数位之前(符号位之后)
- 定点小数:小数点位置在最低数位之后
- 定点整数存在上溢问题(超出表示范围)
- 定点小数存在精度溢出问题(超出表示精度)
- 浮点数
- 表示方法:两个定点数分别表示阶码和尾数
- 溢出问题:存在上溢和下溢问题,也存在精度溢出问题
- 数据分布:浮点数在数轴上的分布并不均匀,越远离原点,浮点数越稀疏
- 浮点运算不满足结合律,小数+大数=大数
- 定点数:包括定点整数和定点小数
真值与机器码比较如下:
| 表示形式 | 机器零 | 用途 | |
|---|---|---|---|
| 真值 | 用”$ + $“和“$ - $”表示符号 | 无 | 无 |
| 原码 | 将符号位加上二进制数的绝对值 | $ +0=000 $$ -0=100 $ | 表示浮点数的尾码 |
| 反码 | 符号位同原码,真值为负数时数值位逐位取反 | $ +0=000 $$ -0=111 $ | 无 |
| 补码 | 真值为负时反码末位加一得到补码 | $ 0=000 $ | 计算机中采用补码进行存储、表示和运算 |
| 移码 | 与补码的符号位相反,数值位相同 | $ 0=100 $ | 表示浮点数的阶码 |
有关补码:
- 补码又称为模2的补码,定点小数的模值为$ 2 $,定点整数的模值为$ 2^{n+1} $;
- 补码的机器零唯一,多表示一个绝对值最大的负数,小数为$ -1 $,整数为$ -2^n $;
- 反码法
- 真值为负数时将原码数据位逐位取反后末位加一得到补码;
- 补码符号位为1时将补码数据位逐位取反后末位加一得到原码;
- 扫描法
- 真值为负数时对原码数据位从右向左扫描,右起第一个1及其右边的数据位不变,其余各位取反。
- 补码符号位为1时对原码数据位从右向左扫描,右起第一个1及其右边的数据位不变,其余各位取反。
有关变形补码:
- 又称为双符号补码,指采用两个符号位表示数据的符号,其余位与补码相同;
- 当符号位为$ 00 $时表示正数,为$ 11 $时表示负数;
- 在运算时,即使产生溢出,变形补码的最高位也永远表示正确的符号位;
- 符号位为$ 01 $表示运算出现正溢出,为$ 10 $时表示出现负溢出。
(2)定点数表示
- 数据表示范围
| 最大正数 | 最小正数 | 最大负数 | 最小负数 | |
|---|---|---|---|---|
| 定点小数 | $ 1-2^{-n} $ | $ 2^{-n} $ | $ -2^{-n} $ | $ -(1-2^{-n}) $,补码表示时为$ -1 $ |
| 定点整数 | $ 2^n-1 $ | $ 1 $ | $ -1 $ | $ -(2^n-1) $,补码表示时为$ -2^n $ |
- 机器码计算公式
| 机器码 | $ -2^n| $ -1 | $ 0\leq x\leq 2^n-1 $或$ 0\leq x\leq 1-2^{-n} $ |
|
|---|---|---|---|
| 原码 | $ 2^n+|x| $ | $ 2+|x| $ | $ x $ |
| 反码 | $ 2^{n+1}+x-1 $ | $ 2+x-2^{-n} $ | $ x $ |
| 补码 | $ 2^{n+1}+x $ | $ 2+x $ | $ x $ |
| 移码 | $ 2^n+x $ | 无 | $ 2^n+x $(整数) |
(3)浮点数表示
表示规则
- $ N=2^{E}\times M=2^E\times\pm(1.m) $
- $ IEEE754 $规则下,浮点数由数符$ S $、阶码$ E $、尾数$ M $三部分组成,阶码采用移码表示,尾数采用原码表示;
- 尾数为定点小数,小数点固定在最左侧,且隐藏小数点左边的$ 1 $,运算时还原为$ 1.M $形式;
- 对于$ 32 $位浮点数($ float $)而言:$ S $为$ 1 $位,$ E $为$ 8 $位,移码偏移为$ 2^7-1 $,$ M $为$ 23 $位;
- 对于$ 64 $位浮点数($ double $)而言:$ S $为$ 1 $位,$ E $为$ 11 $位,移码偏移为$ 2^{10}-1 $,$ M $为$ 52 $位。
转换方法(以$ 32 $位浮点数$ float $为例)
- 将十进制数$ N $转换为$ (-1)^s\times 2^e\times 1.M $,令$ E=e+01111111 $,保存$ S $、$ E $、$ M $;
- 从$ 32 $位二进制串分离出$ S $、$ E $、$ M $,令$ e=E-01111111 $,代入$ (-1)^s\times 2^e\times 1.M $,按权展开。
具体形式说明
- 当阶码为$ 1\sim 254 $时,表示规格化数据;
- 当阶码为$ 255 $时,表示非数或者$ \infty $;
- 当阶码为$ 0 $时,表示机器零或者非规格化数。
| 符号位$ S $ | 阶码$ E $ | 尾数$ M $ | 表示 |
|---|---|---|---|
| $ 0/1 $ | $ 255 $ | 非零 | $ NaN $ |
| $ 0 $ | $ 255 $ | $ 0 $ | $ +\infty $ |
| $ 1 $ | $ 255 $ | $ 0 $ | $ -\infty $ |
| $ 0/1 $ | $ 1\sim 254 $ | $ M $ | $ (-1)^s\times 2^{E-127}\times 1.M $ |
| $ 0/1 $ | 0 | $ M $(非零) | $ (-1)^s\times 2^{-127}\times 0.M $(非规格化数) |
| $ 0/1 $ | $ 0 $ | $ 0 $ | $ +0/-0 $ |
2.非数值数据的表示
(1)字符表示
$ ASCII $码是国际通用的字符码,包含$ 128 $个字符,用**一个字节**表示,最高位为零。(2)汉字编码
汉字编码包含输入码、机内码和字形码,分别用于汉字的输入、汉字在计算机内的存储与处理、汉字的显示和打印;
汉字机内码主要包括$ GB2312 $、$ GBK $、$ GB18030 $、$ Unicode $、$ B1G5 $等标准。
- $ GB2312 $编码
以$ 2 $个字节编码,最高位$ MSB $为$ 1 $;
实际用$ 14 $位表示汉字,采用$ 94\times94 $矩阵表示,每一行为区号,每一列为位号,采用区号+位号的方式得到区位码。
- $ GB2312 $机内码$ = $区位码$ +A0A0H $
3.数据信息的校验
(1)码距
码距:两个编码对应位二进制位不同的个数。
- 编码体系的码距:一个编码体系中所有合法编码的最小码距;
- 码距越大,抗干扰能力、纠错能力越强,数据冗余越大,编码效率越低。
校验码:原始数据$ + $校验数据
(2)奇偶校验
- 编码规则:增加一位校验位,使得数据中的$ 1 $的个数保持奇偶性,利用编码中$ 1 $的个数的奇偶性进行校验;
- 检错性能:奇偶校验码距为$ 2 $,只能检测奇数位错误;
- 可采用交叉奇偶校验提高奇偶校验码的检错与纠错能力,交叉奇偶校验可以检测出所有的$ 3 $位以下错误以及大多数$ 4 $位错误。
- 简单奇偶校验公式:
- 偶校验位:$ P=D_{1}\oplus D_{2}\cdots\oplus D_{n} $
- 偶校验检错位:$ G=D_{1}'\oplus D_{2}'\cdots\oplus D_{n}'\oplus P' $
- 奇校验位:$ P=\overline{D_{1}\oplus D_{2}\cdots\oplus D_{n}} $
- 奇校验检错位:$ G=\overline{D_{1}'\oplus D_{2}'\cdots\oplus D_{n}'\oplus P'} $
- 交叉奇偶校验
- 交叉奇偶校验将待编码的原始数据构造成行列矩阵式结构,同时进行行和列两个方向上的奇偶校验;
- 使每个数据至少位于两个以上的校验组,当校验码中的某一位发生错误时,能在多个检错位中被指出,使得偶数位错误也可以被检查出。
(3)海明校验
①海明编码概述
- 海明编码又称为$ SEC $码;
- $ SEC $码的码距为$ 3 $,只能纠一位错;
- 扩展海明码的码距为$ 4 $,可以检测两位错同时纠正一位错;
- 海明校验是本质上是一种多重奇偶校验,既可以检错也可以纠错。
- 将原始数据信息分成若干偶奇偶校验组,所有数据信息位都会参与两个以上的校验组,每组设置一位偶校验位,所有校验组检错位的值构成检错码;
- 检错码为零,表示数据高概率正确,检错码不为零,则检错码值就是一位错的位置,通过检错码的值就可以实现编码的纠错。
②校验位的位数
设海明码$ N $位,其中数据位$ k $位,校验位$ r $位,有$ N=k+r $,称为$ (n,k) $码;
海明码包含$ r $个偶校验组,$ r $个偶校验组的$ r $检错信息构成一个检错码$ G_r\cdots G_2G_1 $;
为了使其能指出所有一位错,应有$ N=k+r\leq 2^r-1 $,这便是常见的$ ECC $纠错码。
③编码分组规则
设有海明码$ H_n\cdots H_2H_1 $,原始数据$ D_k\cdots D_2D_1 $,校验位$ P_r\cdots P_2P_1 $;
为满足编码分组要求,校验位$ P_i $放在$ H_{2^{i-1}} $位置上,剩余位置由数据位依次填充;
- $ H_i $的数据被编号小于$ i $的若干个海明码位号之和等于$ i $的校验位所校验;
如对于$ (11,7) $码,其编码分组如下:
| $ H_i $ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 映射 | $ P_1 $ | $ P_2 $ | $ D_1 $ | $ P_3 $ | $ D_2 $ | $ D_3 $ | $ D_4 $ | $ P_4 $ | $ D_5 $ | $ D_6 $ | $ D_7 $ |
| 分组 | $ 1 $ | $ 2 $ | $ 1,2 $ | $ 4 $ | $ 1,4 $ | $ 2,4 $ | $ 1,2,4 $ | $ 8 $ | $ 1,8 $ | $ 2,8 $ | $ 1,2,8 $ |
由此根据偶校验规则和各个校验位所校验的数据位,可以得到校验位计算公式:
$ P_1=D_1\oplus D_2\oplus D_4\oplus D_5\oplus D_7 $ $ P_2=D_1\oplus D_3\oplus D_4\oplus D_6\oplus D_7 $ $ P_3=D_2\oplus D_3\oplus D_4 $ $ P_4=D_5\oplus D_6\oplus D_7 $同样可以得到检错位:
$ G_1=D_1'\oplus D_2'\oplus D_4'\oplus D_5'\oplus D_7'\oplus P_1' $ $ G_2=D_1'\oplus D_3'\oplus D_4'\oplus D_6'\oplus D_7'\oplus P_2' $ $ G_3=D_2'\oplus D_3'\oplus D_4'\oplus P_3' $ $ G_4=D_5'\oplus D_6'\oplus D_7'\oplus P_4' $
⑤检错与纠错
- 当检错码$ G_r\cdots G_2G_1=0 $时,表示海明码大概率正确(当出错位数大于等于最小码距时,检错码也可以为$ 0 $);
- $ SEC $码无法区分一位错和两位错;
- 当出现一位错时,检错码的值对应出错的海明码位号,直接取反即可纠错。
⑥扩展海明码
- 又称为$ SECDED $码,最小码距为4,可以区分一位错和两位错,并能纠一位错;
- 在$ SEC $码的基础上添加总偶校验位$ P_{all}=(D_1\oplus D_2\cdots\oplus D_k)\oplus(P_1\oplus P_2\cdots\oplus P_k) $;
- 总偶校验检错码$ G_{all}=P_{all}'\oplus(D_1'\oplus D_2'\cdots\oplus D_k')\oplus(P_1'\oplus P_2'\cdots\oplus P_k') $;
- 检错方法:
- $ G_{all}=0 $且$ G=0 $时,无错误发生;
- $ G_{all}=1 $时,出现一位错,此时如果$ G=0 $,说明$ P_{all} $发生错误,数据部分正确,如果$ G\ne 0 $,说明数据部分发生一位错,可以根据检错码进行纠错;
- $ G_{all}=0 $且$ G\ne 0 $时,出现两位错。
(4)CRC校验
①编码规则
- 利用模$ 2 $运算增加若干位校验位,使得该编码能够被指定的多项式整除;
| 模$ 2 $运算 | 运算法则 |
|---|---|
| 加减法 | 没有进位和借位的二进制加法和减法运算 |
| 乘法 | 根据模$ 2 $加法运算求部分积之和,运算过程中不考虑进位 |
| 除法 | 根据模$ 2 $减法求部分余数 |
除法运算法则:
- 部分余数首位为$ 1 $时,商上$ 1 $,按模$ 2 $运算减除数;
- 部分余数首位为$ 0 $时,商上$ 0 $,减$ 0 $;
- 部分余数小于除数的位数时,该余数即为最后余数;
②$ CRC $校验流程
设有$ CRC $码$ N $位,原始数据$ C_{k-1}\cdots C_1C_0 $共$ k $位,校验位$ P_{r-1}\cdots P_1P_0 $共$ r $位,则$ CRC $码为$ C_{k-1}\cdots C_1C_0P_{r-1}\cdots P_1P_0 $,称为$ (n,k) $码,满足$ N=k+r\leq 2^r-1 $。

③生成$ CRC $编码
假设待发送的$ k $位二进制数据用信息多项式$ M(x) $表示:$ M(x)=C_{k-1}x^{k-1}+C_{k-2}x^{k-2}+\cdots+C_{1}x+C_{0} $;
将$ M(x) $左移$ r $位,得到$ M(x)\cdot 2^r $,右侧空置的$ r $位用来放置校验位;
选择一个$ r+1 $位的生成多项式$ G(x) $,其最高次幂为$ r $,最低次幂为$ 0 $;
用$ M(x)\cdot 2^r $按照模$ 2 $的规则除以$ G(x) $,得到的余数$ R(x) $即为校验码;
设商为$ Q(x) $,则有$ M(x)\cdot 2^r+R(x)=Q(x)G(x)+R(x)+R(X) $,根据模$ 2 $运算有$ R(x)+R(x)=0 $,因此$ M(x)\cdot 2^r+R(x)=Q(x)G(x) $,表明$ CRC $码一定能被$ G(x) $整除,这也是$ CRC $码的编码规则。
生成多项式的规则
- 最高位和最低位均为$ 1 $;
- 当$ CRC $码任何一位发生错误时,都不能被生成多项式整除;
- 不同位发生错误时,余数不同;
- 对余数继续做模$ 2 $运算,应使余数循环。
④$ CRC $编码的循环特性
- $ CRC $编码的非$ 0 $余数具有循环特性,即**将余数左移一位除以生成多项式,将得到下一个余数**,继续重复在新余数基础上左移一位除以生成多项式,多次循环后余数最终能循环为最开始的余数;
- 例如对于$ (7,3) $码,设生成多项式为$ 11101 $,数据位为$ 3 $位,校验码为$ 4 $位,则余数表如下所示:
| 序号 | 编码 | 余数 | 余数值 | 出错位 |
|---|---|---|---|---|
| 1 | $ 0000000 $ | $ 0000 $ | $ 0 $ | 无 |
| 2 | $ 000000\pmb{\underline{1}} $ | $ 0001 $ | $ 1 $ | $ 1 $ |
| 3 | $ 00000\pmb{\underline{1}}0 $ | $ 0010 $ | $ 2 $ | $ 2 $ |
| 4 | $ 0000\pmb{\underline{1}}00 $ | $ 0100 $ | $ \pmb{\underline{4}} $ | $ 3 $ |
| 5 | $ 000\pmb{\underline{1}}000 $ | $ 1000 $ | $ 8 $ | $ 4 $ |
| 6 | $ 00\pmb{\underline{1}}0000 $ | $ 1101 $ | $ 13 $ | $ 5 $ |
| 7 | $ 0\pmb{\underline{1}}00000 $ | $ 0111 $ | $ 7 $ | $ 6 $ |
| 8 | $ \pmb{\underline{1}}000000 $ | $ 1110 $ | $ 14 $ | $ 7 $ |
| 9 | $ 00000\pmb{\underline{11}} $ | $ 0011 $ | $ 3 $ | $ 1+2 $ |
| 10 | $ \pmb{\underline{111}}0000 $ | $ 0100 $ | $ \pmb{\underline{4}} $ | $ 5+6+7 $ |
⑤$ CRC $串行编解码

- 触发器的初始状态均为$ 0 $;
- 有异或门的位置为生成多项式为$ 1 $的位置,如图例得到$ G(x)=x^4+x+1 $,对应编码为$ 10011 $;
- 当$ Q_4=0 $时,不够除,异或门相当于直通,下一个时钟时,数据左移一位;
- 当$ Q_4=1 $时,够除,商上$ 1 $,进行$ Q_4Q_3Q_2Q_1Serial\_in\oplus G(x) $,结果左移。
⑥$ CRC $并行编解码
模$ 2 $除法余数运算满足结合律:两数的余数异或等于两数异或后的余数
$ (M(x)\%G(x))\oplus(N(x)\%G(x))=(M(x)\oplus N(x))\%G(x) $例如:设生成多项式$ G(x)=1011 $,原始数据为$ M(x)=1101 $,传输后的编码为$ 1101\underline{011} $,试求$ CRC $编码和传输后的余数:
- 发送方编码:$ 1101\underline{000}=\pmb{1}000\underline{000}\oplus0\pmb{1}00\underline{000}\oplus000\pmb{1}\underline{000} $,则余数可以由三个数分别对$ G(x) $进行模$ 2 $运算后的余数异或得到;
- 接收方解码:$ 1101\underline{011}=\pmb{1}000\underline{000}\oplus0\pmb{1}00\underline{000}\oplus000\pmb{1}\underline{000}\oplus0000\underline{011} $,同样可以得到对应的余数,其中$ 0000\underline{011} $对$ G(x) $进行模$ 2 $运算后的余数即为$ \underline{011} $;
计算流程
- 先计算$ 2^6 $、$ 2^5 $、$ 2^4 $、$ 2^3 $四个特殊常量的余数,再用余数的组合求解任意编码的余数。
- 在解码时,将计算得到的余数与各个特殊常量的余数比较,若相等,则该特殊常量对应的位出错,纠错即可。