算法设计与分析笔记(二)
四、动态规划
1.基本原理
(1)基本概念
- 最优化问题:这一类问题的可行解可能有很多个。每个解都有一个值,我们希望寻找具有最优值的解(最小值或最大值);
- 最优解可能有多个;
- 根据描述约束条件和目标函数的数学模型的特性和问题的求解方法的不同,可分为:线性规划、整数规划、非线性规划、 动态规划等问题。
(2)动态规划的步骤
问题结构分析:刻画结构特征,给出问题的表示,并明确原始问题;
递推关系建立:分析最优(子)结构特征,构造递推公式;
问题的最优解由相关子问题最优解组合而成,子问题可以独立求解;
递推公式又称状态转移方程。
自底向上计算:确定计算顺序,计算最优解的值;
子问题的无关性和重叠性
- 两个子问题如果不共享资源,它们就是独立的,比如在分治算法中子问题相互独立;
- 重叠是指两个子问题实际上是同一个子问题,只是作为不同问题的子问题出现而已,如果暴力枚举,则会导致大量重叠子问题重复计算。
重叠子问题的解决:动态规划付出额外空间保存结果,对每个子问题只求解一次。
最优方案追踪:利用辅助数组等记录决策过程,输出最优方案。
(3)证明最优子结构性
- 证明问题满足最优性原理是实施动态规划的必要条件。
- 证明的通用模式
- 证明问题最优解的第一个组成部分是做出一个选择,例如,选择钢条第一次切割位置,选择矩阵链的划分位置等。
- 利用“剪切一粘贴”技术证明
- 作为原问题最优解的组成部分,每个子问题的解就是它本身的最优解。
- 利用反证法:假定子问题的解不是其自身的最优解,那么我们就可以从原问题的解中“剪切”掉这些非最优解,将最优解“粘贴”进去,从而得到原问题一个更优的解,这与最初的解是原问题最优解的前提假设矛盾。
(4)备忘机制
为了避免对重叠子问题的重复计算,在递归过程中加入备忘机制。当第一次遇到子问题时,计算其解,并将结果存储在备忘表中;而其后遇到同一个子问题时,通过简单的查表即可返回其解,无需重复计算,节省了时间。
(5)重构最优解
通常定义一个表,记录每个子问题所做的决策。当求出最优解的值后,利用该表回溯即可得到最优方案。
(6)子问题图
- 子问题图用于描述子问题与子问题之间的依赖关系。
- 子问题图是一个有向图,每个顶点唯一地对应一个子问题。
- 若求子问题$ x $的最优解时直接用到子问题$ y $的最优解,则在子问题图中就会有一条从子问题$ x $的顶点到子问题$ y $的顶点的有向边。
- 子问题图是自顶向下递归调用树的“简化版”。
- 在自底向上方法中,对于任何子问题,仅当它依赖的所有子问题都求解完成,才会求解它。
- 子问题的数目等于顶点数;
- 一个子问题的求解时间与子问题图中对应顶点的“出度”成正比;
- 一般情况下,动态规划算法的运行时间与顶点和边的数量至少呈线性关系。
2.01背包问题
(1)问题描述
$ n $个商品组成集合$ O $,每个商品有两个属性$ v_i $和$ p_i $,分别表示体积和价格,背包容量为$ C $试求解一个商品子集$ S\subseteq O $,使得$ max\sum\limits_{i\in S}{p_i} $且$ \sum\limits_{i\in S}{v_i}\leq C $。
(2)问题分析
- 可以选取以下策略:
- 策略1:按商品价格由高到低排序,优先挑选价格高的商品
- 策略2:按商品体积由小到大排序,优先挑选体积小的商品
- 策略3:按商品价值与体积的比由高到低排序,优先挑选比值高的商品
- 以上三种策略都不能达到最优解
(3)暴力枚举
枚举所有组合共$ 2^n-1 $种情况,并检查体积约束
伪代码如下:
$ KnapsackSR(i,c) $:前$ i $个商品中,容量为$ c $时为最优解
时间复杂度为$ O(2^n) $
(4)带备忘递归(自顶向下)
记录子问题解,避免重复计算
伪代码如下:
$ KnapsackMR(i,c) $:带备忘的递归求解
构造备忘录$ P[i,c] $,表示在前$ i $个商品中选择,背包容量为$ c $时的最优解
(5)递推计算(自底向上)
递推公式:$ P[i,c]=max\{P[i-1,c-v[i]]+p[i],P[i-1,c]\} $;
使用$ Rec[i,c] $记录决策过程,选择时为1,否则为0;
回溯解决方案时,倒序判断是否选择商品,根据选择结果,确定最优子问题;
伪代码如下:
$ KnapsackDP(n,p,v,C) $
对数组进行初始化,默认每个商品都不选择;
在$ for $循环中依次计算子问题:
对于每个子问题,如果商品体积$ v[i]\leq c $且选择该商品后得到的总价格$ (P[i-1,c-v[i]]+p[i]) $高,则选择该商品并更新$ P[i,c] $,否则不选择该商品;倒序判断是否选择了该商品,如果选择了该商品,则回溯子问题。
求解表格的算法复杂度为$ O(n\cdot C) $。
※3.最大子数组问题
使用分治算法解决最大子数组问题的时间复杂度为$ O(n\log n) $,使用动态规划方法能达到时间复杂度仅为$ O(n) $的算法。
4.钢条切割问题
(1)问题描述
给定一段长度为$ n $英寸的钢条和一个价格表$ P $,切割工序本身没有成本支出,求切割钢条方案,使得销售收益 $ r_n $ 最大。
假定出售一段长度为i英寸的钢条的价格为$ p_i(i=1,2,\dots) $,下面是价格表$ P $:
(2)问题分析
- 每一英寸都可切割,共有$ n-1 $个切割点,因此长度为$ n $英寸的钢条共有$ 2^{n-1} $中不同的切割方案。
- 如果一个最优解将总长度为$ n $的钢条切割为$ k $段,每段的长度为$ i_j(1\leq j\leq k) $,则有$ n=i_1+i_2+\dots+i_k $,得到的最大收益为$ r_n=p_{i_1}+p_{i_2}+\dots+p_{i_k} $
- 首次切割后,将两段钢条看成两个独立的钢条切割问题实例。若分别获得两段钢条的最优切割收益$ r_j $和$ r_{n-j} $,则原问题的解就可以通过组合这两个相关子问题的最优子解获得。
- 也即最优子结构性——如果$ r_n=r_i+r_{n-i} $是最优切割收益,则$ r_i $、$ r_{n-i} $是相应子问题的最优切割收益。
(3)朴素递归
- $ r_n=\max\limits_{1\leq i\leq n}{(p_i+r_{n-i})} $
运行效率很差,存在一些相同的子问题重复调用解决
- $ T(n)=1+\sum\limits_{j=0}^{n-1}{T(j)} $,也即$ T(n)=2^n $
(4)带备忘递归(自顶向下)
依旧按照递归的形式编写过程,但处理过程中会保存每个子问题的解。
具体实现如下:
其中辅助数组$ r[0\dots n] $用于保存子问题的结果。
初始化为$ -\infty $;
当有新的结果时,$ r[n] $保存结果$ q $;
当$ r[n]\geq 0 $时,直接引用其中已保存的值。
运行时间为$ \Theta(n^2) $
(5)自底向上
将子问题按规模排序,按由小到大的顺序顺次求解,当求解某个子问题时,它所依赖的更小子问题都已求解完毕,结果已经保存,故可以直接引用并组合出它自身的解
运行时间为$ \Theta(n^2) $,相比自顶向下的方法具有更小的系数
(6)自底向上(给出切割方案)


5.矩阵链乘法问题
(1)基本背景
- 已知$ A $为$ p\times r $的矩阵,$ B $为$ r\times q $的矩阵,则$ A $与$ B $的乘积是一个$ p\times q $的矩阵,矩阵相乘需要进行$ pqr $次标量乘法运算。
- $ n $个要连续相乘的矩阵构成一个矩阵链$ \langle A_1,A_2,\dots,A_n\rangle $,要计算这$ n $个矩阵的连乘乘积:$ A_1A_2\dots A_n $,称为矩阵链乘问题。
- 矩阵链乘满足结合律,不满足交换律。
- 不同的加括号方式代表不同的计算模式,而不同的计算模式计算矩阵链乘积的代价不同。
(2)问题描述
- 给定$ n $个矩阵的链,记为$ \langle A_1,A_2,\dots,A_n\rangle $,其中$ i=1,\dots,n $,矩阵$ A_i $的维数为$ p_{i-1}\times P_i $。
- 求“完全括号化方案”,使得计算乘积$ A_1A_2\dots A_n $所需的标量乘法次数最小。
- 穷举所有方案的数量:当$ n=1 $时,$ P(n)=1 $,当$ n\geq 2 $时,$ P(n)=\sum\limits_{k=1}^{n-1}{P(k)P(n-k)} $,证明得到时间复杂度为$ P(n)=\Omega(2^n) $
(3)动态规划
最优括号化方案的结构特征——寻找最优子结构
- 整体的最优括号化方案可以通过寻找使最终标量乘法次数最小的两个最优括号化子方案得到,形如:$ (A_1A_{i+1}\dots A_k)(A_{k+1}\dots A_n) $
递推求解方案
- 递推求解公式
- 使用$ s[i,j] $保存$ A_iA_{i+1}\dots A_j $最优括号化方案的分割点位置$ k $
计算最优代价
对应子问题为$ \Theta(n^2) $个,存在子问题重叠现象,同最优子结构性一样,这也是应用动态规划的标识。
采用自底向上法替代该递推求解公式
算法的输入为序列$ p=\langle p_0,p_1,\dots,p_n\rangle $,长度为$ p.length=n+1 $
算法伪代码如下:
第$ 3\thicksim 4 $行计算$ m[i,i]=0 $
第$ 5\thicksim 13 $行计算不同矩阵链长度下$ m[i,i+l-1] $的最小计算代价,长度依次递增计算。
可以使用一个上三角矩阵表表示$ m[i,j] $和$ s[i,j] $
具体实例如下:
算法运行时间为$ \Omega(n^3) $,空间复杂度为$ \Theta(n^2) $
构造最优解
- $ s[i,j] $记录了$ A_iA_{i+1}\dots A_j $的最优括号化方案的“首个”分割点$ k $。基于$ s[i,j] $,对$ A_iA_{i+1}\dots A_j $的括号化方案是:
$ (A_iA_{i+1}\dots A_{s[i,j]})(A_{s[i,j]+1}\dots A_j) $
打印结果的伪代码如下:
- $ s[i,j] $记录了$ A_iA_{i+1}\dots A_j $的最优括号化方案的“首个”分割点$ k $。基于$ s[i,j] $,对$ A_iA_{i+1}\dots A_j $的括号化方案是:
6.最长公共子序列
(1)基本背景
子序列
给定两个序列$ X=\langle X_1,X_2,\dots,X_n\rangle $和序列$ Z=\langle z_1,z_2,\dots,z_k\rangle $,若存在$ X $的一个严格递增下标序列$ \langle i_1,i_2,\dots,i_k\rangle $,使得对所有$ j=1,2,\dots,k $,有$ x_{i_j}=z_j $,则称$ Z $是$ X $的子序列。
$ Z=\langle B,C,D,B\rangle $是$ X=\langle A,B,C,B,D,A,B\rangle $的一个子序列,对应下标序列为$ \langle 2,3,5,7\rangle $。
公共子序列
对给定的两个序列$ X $和$ Y $,若序列$ Z $既是$ X $的的子序列,也是$ Y $的子序列,则称$ Z $是$ X $和$ Y $的公共子序列。
$ X=\langle A,B,C,B,D,A,B\rangle $,$ Y=\langle B,D,C,A,B,A\rangle $,则序列$ \langle B,C,A\rangle $是$ X $和$ Y $的一个公共子序列。
最长公共子序列(LCS)
两个序列的长度最大的公共子序列称为它们的最长公共子序列。
$ \langle B,C,A\rangle $是上面$ X $和$ Y $的一个公共子序列,但不是$ X $和$ Y $的最长公共子
序列。最长公共子序列是$ \langle B,C,B,A\rangle $。
前缀
给定一个序列$ X=\langle x_1,x_2,\dots,x_m\rangle $,对于$ i=0,1,\dots,m $,定义$ X $的第$ i $个前缀为$ X_i=\langle x_1,x_2,\dots,x_i\rangle $,即前$ i $个元素构成的子序列。
$ X=\langle A,B,C,B,D,A,B\rangle $,则$ X_4=\langle A,B,C,B\rangle $,$ X_0=\Phi $。
(2)最优子结构性
两个序列的一个$ LCS $也包含了两个序列的前缀的$ LCS $,即$ LCS $问题具有最优子结构性质。
定理:设有序列$ X=\langle x_1,x_2,\dots,x_m\rangle $和$ Y=\langle y_1,y_2,\dots,y_n\rangle $,并设序列$ Z=\langle z_1,z_2,\dots,z_k\rangle $为$ X $和$ Y $的任意一个$ LCS $。
(1)若$ x_m=y_n $,则$ z_k=x_m=y_n $,且$ Z_{k-1} $是$ X_{m-1} $和$ Y_{n-1} $的一个$ LCS $。
(2)若$ x_m\ne y_n $,则$ z_k\ne x_m $蕴含$ Z $是$ X_{m-1} $和Y的一个$ LCS $。
(3)若$ x_m\ne y_n $,则$ z_k\ne y_n $蕴含$ Z $是$ X $和$ Y_{n-1} $的一个$ LCS $。
(3)递推关系式
记$ c[i,j] $为前缀序列$ X_i $和$ Y_j $的一个$ LCS $的长度,则有

1)若$ i=0 $或$ j=0 $,即其中一个序列的长度为零,则$ LCS $的长度为0,$ LCS=\Phi $;
2)若$ x_i=y_j $,则$ X_i $和$ Y_j $的$ LCS $是在$ X_{i-1} $和$ Y_{j-1} $的$ LCS $之后附加将$ x_i $得到的,所以
$ c[i,j]=c[i-1,j-1]+1 $;3)若$ x_i\ne y_j $,则$ X_i $和$ Y_j $的$ LCS $的最后一个字符不会是$ x_i $或$ y_j $(不可能同时等于两者,或与两者都不同),此时该$ LCS $应等于$ X_{i-1} $和$ Y_j $的$ LCS $与$ X_i $和$ Y_{j-1} $的$ LCS $之中的较长者。所以
$ c[i,j]=max(c[i-1,j],c[i,j-1]) $。
(4)自底向上
过程$ LCS-LENGTH(X,Y) $用来求序列$ X=\langle x_1,x_2,\dots,x_m\rangle $和$ Y=\langle y_1,y_2,\dots,y_n\rangle $的$ LCS $的长度,其时间复杂度为$ O(mn) $。
表$ c[1..m,1..n] $中包含每一阶段的$ LCS $长度,$ c[m,n] $等于$ X $和$ Y $的$ LCS $的长度。
表$ b[1..m,1..n] $记录当前$ c[i,j] $的计值情况,以此来构造该$ LCS $。
下图给出了在$ X=\langle A,B,C,B,D,A,B\rangle $和$ Y=\langle B,D,C,A,B,A\rangle $上运行$ LCS-LENGTH $计算出的表:
1)第$ i $行和第$ j $列中的方块包含了$ c[i,j] $的值以及$ b[i,j] $记录的箭头。
2)对于$ i,j>0 $,项$ c[i,j] $仅依赖于是否有$ x_i=y_j $及项$ c[i-1,j] $、$ c[i,j-1] $、$ c[i-1,j-1] $的值。
3)为了重构一个$ LCS $,从右下角开始跟踪$ b[i,j] $箭头即可
4)图中,$ c[7,6]=4 $,$ LCS(X,Y)=\langle B,C,B,A\rangle $。
(5)构建最优解
借助$ b[i,j] $反序输出$ LCS $,由于每一次循环使$ i $或$ j $减1,最终$ m=0 $,$ n=0 $,算法结束,所以$ PRINT-LCS $的时间复杂度为$ O(m+n) $。
改进:去掉表$ b $,直接基于$ c $求$ LCS $
1
2
3
4
5
6
7
8
9
10PRINT-LCS-WITHOUTAUXI(c, X, Y, i, j)
if c[i, j] == 0
return
if X[i] == Y[j]
PRINT-LCS-WITHOUTAUXI(c, X, Y, i - 1, j - 1)
print X[i]
else if c[i - 1, j] >= c[i, j - 1]
PRINT-LCS-WITHOUTAUXI(c, X, Y, i - 1, j)
else
PRINT-LCS-WITHOUTAUXI(c, X, Y, i, j - 1)改进:算法中,每个$ c[i,j] $的计算仅需$ c $的两行的数据:正在被计算的一行和前面的一行。
※7.最长公共子串
8.最优二叉搜索树
(1)基本背景
二叉搜索树$ T $是一棵二元树,它或者为空,或者其每个结点含有一个可以比较大小的数据元素,且有:
- $ T $的左子树的所有元素比根结点中的元素小;
- $ T $的右子树的所有元素比根结点中的元素大;
- $ T $的左子树和右子树也是二叉搜索树。
给定一个$ n $个关键字的升序序列$ K=\langle k_1,k_2,\dots,k_n\rangle $,对每个关键字$ k_i $,都有一个概率$ p_i $表示其被搜索的频率。根据$ k_i $和$ p_i $构建一个二叉搜索树$ T $,每个$ k_i $对应树中的一个结点。
引入外部结点$ d_0,d_1,\dots,d_n $,用来表示不在$ K $中的值,称为伪关键字。
伪关键字在$ T $中对应外部结点,共有$ n+1 $个。
扩展二叉树:内结点表示关键字$ k_i $,外结点(叶子结点)表示$ d_i $。
每个$ d_i $代表一个区间,$ d_0 $表示所有小于$ k_1 $的值,$ d_n $表示所有大于$ k_n $的值,对于$ i=1,\dots,n-1 $,$ d_i $表示所有在$ k_i $和$ k_{i+1} $之间的值。
每个$ d_i $也有一个概率$ q_i $,表示搜索对象$ x $恰好落入区间$ d_i $的频率。
一次搜索的代价等于从根结点开始访问结点的数量(包括外部结点)
从根结点开始访问结点的数量等于结点在$ T $中的深度+1,记$ depth_{T(i)} $为结点$ i $在$ T $中的深度
二叉搜索树$ T $的期望代价为
最优二叉搜索树:对于给定的关键字及其概率集合,期望搜索代价最小的二叉搜索树。
(2)动态规划
最优二叉搜索树的最优子结构
如果$ T $是一棵相对于关键字$ k_1,\dots,k_n $和伪关键字$ d_0,\dots,d_n $的最优二叉搜索树,则$ T $中一棵包含关键字$ k_i,\dots,k_j $的子树$ T’ $必然是相对于关键字$ k_i,\dots,k_j $(和伪关键字$ d_{i-1},\dots,d_j $)的最优二叉搜索子树。
构造最优二叉搜索树
求解包含关键字$ k_i,\dots,k_j $的最优二叉搜索树,其中$ i\geq 1 $,$ j\leq n $且 $ j\geq i-1 $
定义$ e[i,j] $:为包含关键字$ k_i,\dots,k_j $的最优二叉搜索树的期望搜索代价。
当$ j=i-1 $时,由于子树只包含伪关键字$ d_{i-1} $,期望搜索代价为$ e[i,i-1]=q_{i-1} $
当$ j\geq i $时,从$ k_i,\dots,k_j $中选择出根结点$ k_r $,以此构建两个最优左右二叉搜索子树。
计算期望搜索代价
定义$ root[i,j] $,保存计算$ e[i, j] $时,使$ e[i, j] $取得最小值的$ r $,$ k_r $即为关键字$ k_i,\dots,k_j $的最优二叉搜索(子)树的树根。在求出$ e[1,n] $后,利用$ root $即可构造出最终的最优二叉搜索树。
- $ w[1..n+1,0..n] $用于保存子树的结点概率之和,每个$ w[i,j] $的计算时间仅为$ \Theta(1) $
满足
自底向上的迭代计算,时间复杂度为$ \Theta(n^3) $





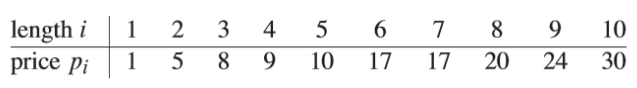












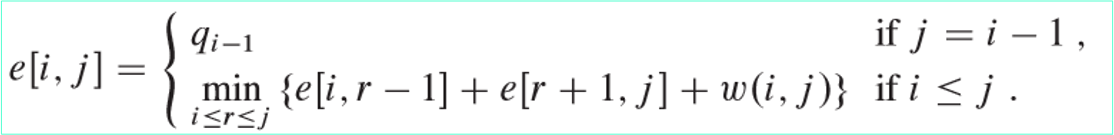
![BST-w[i,j]](https://picbed.cloudchewie.com/blog/post/Algorithm-Design-and-Analysis-2/Chp4-BST-w%5Bi%2Cj%5D.png!blogimg)



