强化学习笔记(二)
二、经典强化学习
2.3 蒙特卡洛方法
2.3.1 蒙特卡洛方法
基本思想
- 动态规划用于解决已知的 MDP 问题(Model-Based)
- 而如何解决未知的 MDP(Model-Free)
- Model-Free Prediction:评估值函数,如蒙特卡洛方法、时间差分学习 TD
- Model-Free Control:优化值函数,如 On-Policy 蒙特卡洛方法、On-Policy 时间差分学习
蒙特卡洛方法的特点
- 核心思想:基于一个朴素的假设——价值函数等于回报的平均值
- 模型无关(Model-Free):不需要知道 MDP 的状态转移概率$ P(s^{\prime}, r\mid s, a) $ 或奖励函数,仅从采样的交互数据中学习
- 直接从完整的经验片段(episode)中学习:使用整个回合的经验来更新估计,即从起点到终点的所有交互,而不是依赖于部分的价值函数估计
2.3.2 蒙特卡洛策略评估
- 蒙特卡洛策略评估
- 实现步骤
- 收集经验片段:运行策略$ \pi $,采样多个完整片段$ S_1,A_1,R_2,\cdots,S_k $,直到回合结束
- 计算回报:在每个时间步$ t $,计算从$ t $开始到回合结束的折扣回报$ G_t $
- 更新价值函数,将每次访问状态$ s $时的$ G_t $取平均,作为$ v_{\pi}(s) $ 的估计
- 使用经验回报的样本均值替代期望回报:$ v_{\pi}(s)\approx \frac{1}{N(s)} \displaystyle\sum_{i=1}^{N(s)} G_t^{(i)} $
- 其中$ N(s) $是状态$ s $在采样中被访问的次数,$ G_t^{(i)} $是状态$ s $的第$ i $ 次回报
- 必须要等到一个 episode 结束,才可以进行估计更新
- 如何对同一个状态进行计数
- First-Visit:在一个 episode 中,只记录某个状态第一次出现时的回报
- Every-Visit:在一个 episode 中,记录某个状态每次出现时的回报
- 实现步骤
- 增量蒙特卡洛
- Online:每次进行采样时,逐步更新价值估计,$ \mu_k=\mu_{k-1}+\frac{1}{k}(x_k-\mu_{k-1}) $
- 对于每个回报为$ G_t $的状态$ S_t $ $$ \begin{aligned} N(S_t)&\gets N(S_t)+1\\ V(S_t)&\gets V(S_t)+\frac{1}{N(S_t)}(G_t-V(S_t)) \end{aligned} $$
- 对于非平稳问题:$ V(S_t)\leftarrow V(S_t)+\alpha\left(G_t-V(S_t)\right) $
2.3.3 蒙特卡洛控制
On-Policy 蒙特卡洛控制(Monte-Carlo Control)
利用价值函数用贪心进行策略改进需要 MDP 模型,而利用动作值函数则是 Model-Free 的
$$ \begin{aligned} \pi^{\prime}(s)&=\underset{a\in\mathcal{A}}{\operatorname*{\operatorname*{argmax}}}R_s^a+P_{ss^{\prime}}^aV(s^{\prime})\\ \pi^{\prime}(s)&=\underset{a\in\mathcal{A}}{\operatorname*{\operatorname*{\arg\max}}}Q(s,a) \end{aligned} $$采用$ \epsilon $-贪心策略:$ 1-\epsilon $的概率选择贪心动作,$ \epsilon $的概率选择随机动作,即
$$ \pi(a\mid s)=\left\{ \begin{array} {ll}\epsilon/m+1-\epsilon & \mathrm{if}\quad a^*=\arg\max Q(s,a) \\ \epsilon/m & \mathrm{otherwise} \end{array}\right. $$- $ \epsilon $-贪心策略的证明 $$ \begin{aligned} v_{\pi^\prime}(s)=q_\pi(s,\pi^{\prime}(s)) & =\sum_{a\in\mathcal{A}}\pi^{\prime}(a\mid s)q_\pi(s,a) \\ & =\epsilon/m\sum_{a\in\mathcal{A}}q_\pi(s,a)+(1-\epsilon)\max_{a\in\mathcal{A}}q_\pi(s,a) \\ & \geq\epsilon/m\sum_{a\in\mathcal{A}}q_\pi(s,a)+(1-\epsilon)\sum_{a\in\mathcal{A}}\frac{\pi(a\mid s)-\epsilon/m}{1-\epsilon}q_\pi(s,a) \\ & =\sum_{a\in\mathcal{A}}\pi(a\mid s)q_\pi(s,a)=v_\pi(s) \end{aligned} $$
算法流程
初始化:
- 动作价值函数 $ Q(s, a) = 0 $
- 计数器 $ N(s, a) = 0 $
- 初始策略 $ \pi $ 为随机策略
循环直到收敛(对于每个 episode):
- 根据当前策略 $ \pi $ 执行一次完整的轨迹$ S_1, A_1, R_2, S_2, A_2, R_3, \ldots, S_T $。
- 对轨迹中的每个状态-动作对 $ (s, a) $:
- 计算从该状态起始的回报 $ G_t $
- 更新计数器 $ N(s, a) $:
$$
N(s, a) \leftarrow N(s, a) + 1
$$ - 更新动作价值函数:
$$
Q(s, a) \leftarrow Q(s, a) + \frac{1}{N(s, a)} \left[ G_t - Q(s, a) \right]
$$
- 更新策略为 $ \epsilon $-贪婪策略:
- 以 $ 1 - \epsilon $ 概率选择贪婪动作
- 以 $ \epsilon $ 概率随机探索
Greedy in the Limit with Infinite Exploration(GLIE)
- 确保每个状态-动作对都被无限次访问
- 确保策略收敛至贪婪策略
- 取$ \epsilon=\frac{1}{N(s, a)} $
- 性质与收敛性
- 探索性:随着 $ t \to \infty $,通过 $ \epsilon $-贪婪策略,每个状态-动作对 $ (s, a) $ 都会被无限次访问
- 利用性:随着 $ \epsilon \to 0 $,策略逐渐变为贪婪策略,并优化为最优策略
- 收敛性:GLIE 符合强化学习的收敛条件,最终保证 $ Q(s, a) \to q^{\star}(s, a) $,并找到最优策略 $ \pi^{\star} $
2.4 时间差分学习(TD)
2.4.1 时间差分学习
- 特点
- 直接从经验中学习:TD 方法通过与环境的交互,不依赖于模型,是模型无关的
- 学习自不完全回合:TD 方法能够在回合尚未结束时进行学习,即在回合的中间就开始更新估计
- 引导(Bootstrapping)
- TD 使用当前对值函数的估计来更新自己,而不是依赖最终的回报。这是与蒙特卡洛方法的根本区别
- 每次更新不仅仅依赖于一个实际的回报,而是基于当前状态和动作的估计,以及下一状态的价值估计
- 使用当前的估计值来更新状态的价值函数,即$ V(S_t)\leftarrow V(S_t)+\alpha\left(R_{t+1}+\gamma V(S_{t+1})-V(S_t)\right) $
- TD 目标:$ R_{t+1}+\gamma V(S_{t+1}) $,即预估的回报
- TD 误差:$ \delta_t=R_{t+1}+\gamma V(S_{t+1})-V(S_t) $
- 更新过程:TD 方法的更新是通过将一个“猜测”更新到另一个“猜测”。具体来说,TD 更新的是值函数的估计,依赖于当前的估计以及环境的即时反馈。
- 蒙特卡洛方法与 TD 方法的形象对比
- 蒙特卡洛方法:像看完一部电影后写影评
- 蒙特卡洛方法就像一个影评人,必须把整部电影看完,从头到尾看清所有情节,才能写出一篇完整的影评。
- 比如你想知道某个演员在电影中的表现有多好,影评人会等电影结束后,回想起演员在不同场景中的表现,然后总结打分。这相当于在强化学习中,蒙特卡洛方法等到整个回合(从初始状态到终止状态)结束后,再回过头来计算每个状态的价值。
- 时序差分方法:像追剧时边看边预测剧情
- 时序差分方法就像一个追剧爱好者,每看一集就开始预测下一集剧情,然后用下一集的内容来调整自己的预测。
- 比如你在看电视剧,看到男主角一脸愁容时,你预测接下来他会有重大打击。看了下一集发现他真的失业了,你会根据这个信息修正自己的预测。TD 方法就是根据“当前的状态价值”加上“下一个状态的反馈”,不断调整估计。
- 蒙特卡洛方法:像看完一部电影后写影评
- 偏差(bias)和方差(variance)的权衡
- $ G_t $是$ v_{\pi}(S_t) $的无偏估计
- $ G_t $的方差较大,因为它依赖于多个随机因素(动作、状态转移和奖励)
- 真 TD 目标$ R_{t+1}+\gamma V_{\pi}(S_{t+1}) $也是$ v_{\pi}(S_t) $的无偏估计
- TD 目标$ R_{t+1}+\gamma V(S_{t+1}) $则是$ v_{\pi}(S_t) $ 的有偏估计
- TD 目标的方差较小,因为它只依赖于一个时间步的随机因素(即时奖励和下一状态的估计),并且通过引导更新逐步减少方差
- 区别
- TD 可以在知道最终结果前进行学习
- TD 可以在不知道最终结果的情况下学习
- TD 可以从不完整的序列中学习
- TD 可以在线学习,每一步之后更新
- TD 利用了马尔可夫性质,隐式地构建最大似然马尔可夫过程
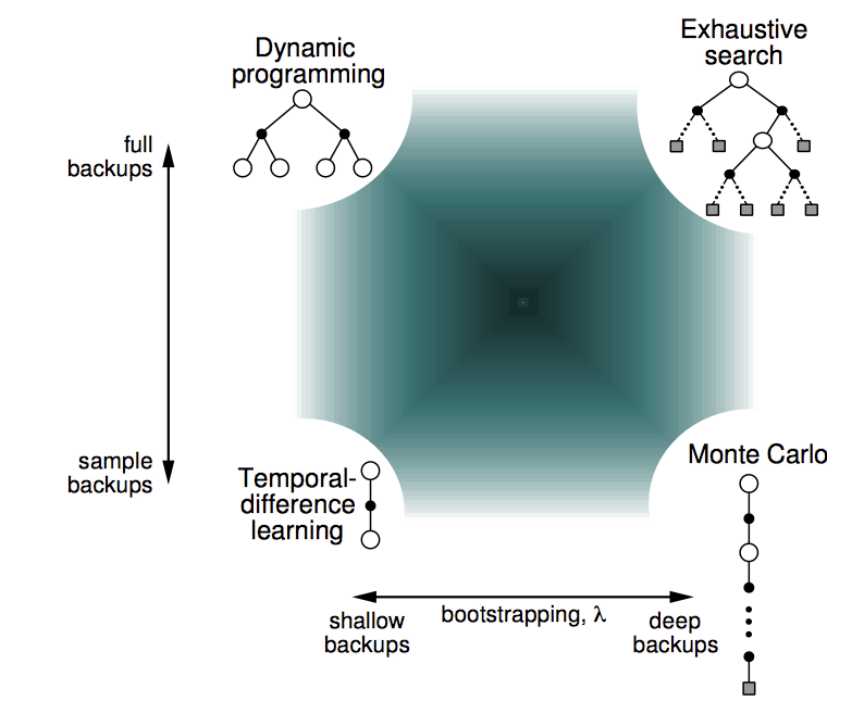
- Bootstrapping 和 Sampling(引导和采样)
- Bootstrapping:在更新估计时,利用当前的估计值来计算新的估计值
- MC 不进行 Bootstrap,而 DP 和 TD 进行
- Sampling:是否通过从环境中采样来估计期望值
- DP 算法是 No Sampling 的,它需要完全了解环境动态,详细地知道每种可能性,即 Full Backup
- MC 和 TD 是 Sampling 的,它们只需要从环境中采样,即 Sample Backup
- Bootstrapping:在更新估计时,利用当前的估计值来计算新的估计值
2.4.2 TD($ \lambda $)
基本思想
- 让 TD 目标猜测未来$ n $步 $$ \begin{aligned} (TD)\quad n=1\quad & G_{t}^{(1)}=R_{t+1}+\gamma V(S_{t+1}) \\ n=2\quad & G_{t}^{(2)}=R_{t+1}+\gamma R_{t+2}+\gamma^{2}V(S_{t+2}) \\ (MC)\quad n=\infty\quad & G_{t}^{(\infty)}=R_{t+1}+\gamma R_{t+2}+...+\gamma^{T-1}R_{T} \end{aligned} $$
- $ n $步回报:$ G_{t}^{(n)}=R_{t+1}+\gamma R_{t+2}+\cdots+\gamma^{n}V(S_{t+n}) $
- $ n $步 TD 学习:$ V(S_t )\gets V(S_t)+\alpha(G_t^{(n)}-V(S_t)) $
合并来自所有不同时间步的信息——引入$ \lambda $
- $ \lambda $-回报:$ G_t^{\lambda}=(1-\lambda)\displaystyle\sum_{n=1}^{\infty}\lambda^{n-1}G_t^{(n)} $
- 如果$ \lambda=0 $,则整体更新减少到其第一个分量,即一步 TD 更新
- 如果$ \lambda=1 $,则整体更新减少到其最后一个分量,即蒙特卡洛更新
- 前向 TD($ \lambda $)
- $ V(S_t )\gets V(S_t)+\alpha(G_t^{\lambda}-V(S_t)) $
- 需要在完整的回合之后计算,无法在线更新
- 后向 TD($ \lambda $)
- 资格迹(Eligibility traces)
- 用于记忆
- 在时间步$ t $,状态$ s $的资格迹为$ E_t(s)\in \mathbb{R}^+ $ $$ \begin{aligned} E_t(s)&=\gamma\lambda E_{t-1}(s),\quad\forall s\in\mathcal{S},s\ne S_t \\ E_t(S_t)&=\gamma\lambda E_{t-1}(S_t)+1\\ E_t(s)&= \gamma\lambda E_{t-1}(s) + \mathbf{1}(S_t=s) \end{aligned} $$
- 称$ \lambda $为迹衰减参数
- 资格迹记录了最近哪些状态或动作对当前学习目标的重要性
- 资格迹值越高,该状态的价值函数(或动作值函数)就越需要根据当前的强化信号(如奖励)进行更新 $$ \begin{aligned} \delta_t=R_{t+1}+\gamma V(S_{t+1})-V(S_t)\\ V(S_t )\gets V(S_t)+\alpha\delta_t E_t(s) \end{aligned} $$
- 资格迹(Eligibility traces)
- 后向 TD($ \lambda $)的特殊情况
- 当$ \lambda=0 $时,$ E_t(s)=\mathbf{1}(S_t=s) $,仅有当前状态被更新,退化为$ \text{TD}(0) $
- 当$ \lambda=1 $时,$ E_t(s)=\displaystyle\sum_{k=0}^{\infty}\gamma^k1(S_{t+k}=s) $,退化为 MC 或称为$ \text{TD}(1) $
- $ \text{TD}(1) $与 MC 方法
- 对于$ \text{TD}(\lambda) $ $$ \begin{aligned} E_{t}(s) & =\gamma\lambda E_{t-1}(s)+\mathbf{1}(S_{t}=s) \\ & =\left\{ \begin{array} {ll}0 & \mathrm{~if~}t\lt k \\ (\gamma\lambda)^{t-k} & \mathrm{~if~}t\geq k \end{array}\right. \end{aligned} $$
- $ \text{TD}(1) $能够在线更新累计误差 $$ \sum_{t=1}^{\mathcal{T}-1}\alpha\delta_{t}E_{t}(s)=\alpha\sum_{t=k}^{\mathcal{T}-1}\gamma^{t-k}\delta_{t}=\alpha\left(G_{k}-V(S_{k})\right) $$
- 而最终的累计误差即为 MC 误差 $$ \begin{aligned} & \delta_t+\gamma\delta_{t+1}+\gamma^2\delta_{t+2}+...+\gamma^{T-1-t}\delta_{T-1} \\ & =R_{t+1}+\gamma V(S_{t+1})-V(S_t) \\ & +\gamma R_{t+2}+\gamma^2V(S_{t+2})-\gamma V(S_{t+1}) \\ & +\gamma^2R_{t+3}+\gamma^3V(S_{t+3})-\gamma^2V(S_{t+2}) \\ & +\gamma^{T-1-t}R_{T}+\gamma^{T-t}V(S_{T})-\gamma^{T-1-t}V(S_{T-1}) \\ & =R_{t+1}+\gamma R_{t+2}+\gamma^2R_{t+3}...+\gamma^{T-1-t}R_T-V(S_t) \\ & =G_t-V(S_t) \end{aligned} $$
- $ \text{TD}(1) $大致相当于 Every-Visit 蒙特卡洛
- 对于一般的$ \lambda $,TD 误差也会累积到$ \lambda $-误差,即$ G^\lambda_t-V(S_t) $
- $ \lambda $-回报:$ G_t^{\lambda}=(1-\lambda)\displaystyle\sum_{n=1}^{\infty}\lambda^{n-1}G_t^{(n)} $
前向与后向$ \text{TD}(\lambda) $的对比
离线
Offline Updates $\lambda = 0$ $\lambda \in (0, 1)$ $\lambda = 1$ Backward View TD(0) TD($ \lambda $) = TD(1) = Forward View TD(0) Forward TD($ \lambda $) MC 在线
Online Updates $ \lambda = 0 $ $ \lambda \in (0, 1) $ $ \lambda = 1 $ Backward View TD(0) TD($ \lambda $) $ \ne $ TD(1) $ \ne $ Forward View TD(0) Forward TD($ \lambda $) = MC = Exact Online TD(0) Exact Online TD($ \lambda $) Exact Online TD(1)
2.4.3 TD 控制(SARSA)
基本思想
- On-Policy 的 TD 控制(SARSA)
- 应用 TD 到$ Q(S,A) $中
- 每一个时间步均进行更新
初始化:
- 动作值函数 $ Q(s, a) $ 随机初始化
- $ \epsilon $-贪婪策略初始化
循环更新(对于每个时间步):
- 从起始状态 $ S_0 $ 开始
- 根据 $ \epsilon $-贪婪策略选择动作 $ A_t $
- 执行动作 $ A_t $,观察奖励 $ R_{t+1} $ 和下一状态 $ S_{t+1} $
- 根据策略选择下一动作 $ A_{t+1} $
- 更新动作值函数: $$ Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \alpha \left( R_{t+1} + \gamma Q(S_{t+1}, A_{t+1}) - Q(S_t, A_t) \right) $$
- 将状态和动作更新为 $ S_{t+1} $ 和 $ A_{t+1} $
- 重复直到达到终止状态
更新策略:使用新的 $ Q(s, a) $ 利用贪婪算法改进策略
SARSA 的收敛性:SARSA 收敛于最优动作值函数,即$ Q(s,a)\rightarrow q_*(s,a) $,当满足
- GLIE 性质
2.4.4 SARSA($ \lambda $)
考虑多步回报
$$ \begin{aligned} (SARSA)\quad n=1\quad & q_{t}^{(1)}=R_{t+1}+\gamma Q(S_{t+1}) \\ n=2\quad & q_{t}^{(2)}=R_{t+1}+\gamma R_{t+2}+\gamma^{2}Q(S_{t+2}) \\ (MC)\quad n=\infty\quad & q_{t}^{(\infty)}=R_{t+1}+\gamma R_{t+2}+...+\gamma^{T-1}R_{T} \end{aligned} $$- $ n $步 Q 回报:$ q_{t}^{(n)}=R_{t+1}+\gamma R_{t+2}+\cdots+\gamma^{n}Q(S_{t+n}) $
- $ n $步 SARSA:$ Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha\left(q_t^{(n)}-Q(S_t,A_t)\right) $
引入$ \lambda $
- $ \lambda $-Q 回报:$ q_t^\lambda=(1-\lambda)\displaystyle\sum_{n=1}^\infty\lambda^{n-1}q_t^{(n)} $
前瞻性 SARSA($ \lambda $)
- 从“未来回报”的视角计算状态-动作值函数的更新
- $ Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha\left(q_t^{\lambda}-Q(S_t,A_t)\right) $
- 由于需要计算$ n $-步回报,前瞻性 SARSA($ \lambda $) 必须等待整个回合结束才能更新动作值函数
- 无法在线更新
后瞻性 TD($ \lambda $)
- 从“过去的状态-动作对对当前 TD 误差的影响”的视角出发
- 将 TD 误差 $ \delta_t $ 不仅用于更新当前状态-动作对,还用于调整所有之前访问过的状态-动作对
- $ E_t(s,a) $是资格迹(Eligibility Traces),表示某状态-动作对与当前学习更新的相关性
- 对所有状态-动作对初始化,$ E_t(s,a)=0 $
- 更新规则为$ E_t(s,a)\gets \gamma\lambda E_{t-1}(s,a)+\mathbf{1}(S_t=s,A_t=a) $
- 对动作值函数进行更新
$$
\begin{aligned}
\delta_t=R_{t+1}+\gamma Q(S_{t+1},A_{t+1})-Q(S_t,A_t)\
Q(s,a)\leftarrow Q(s,a)+\alpha\delta_tE_t(s,a)
\end{aligned}
$$ - 按时间步更新,无需完整的轨迹,可以逐步在线更新值函数,效率高
2.5 Q-Learning
基本思想
- Off-Policy 学习
- 希望观察他人的行为/利用旧策略来学习
- 希望遵循探索性策略来学习最优策略
- 希望遵循一个策略来学习多个策略
形式化定义
- 设行为策略$ \mu(a\mid s) $ $$ \{S_1,A_1,R_2,...,S_T\}\sim\mu $$
- 目标:遵循行为策略,评估/改进目标策略$ \pi(a\mid s) $
重要性采样(Importance Sampling)
如何估计另一个分布的期望
$$ \begin{aligned} \mathbb{E}_{X\sim P}[f(X)] & =\sum P(X)f(X) \\ & =\sum Q(X)\frac{P(X)}{Q(X)}f(X) \\ & =\mathbb{E}_{X\sim Q}\left[\frac{P(X)}{Q(X)}f(X)\right] \end{aligned} $$离策略蒙特卡洛
- 利用从$ \mu $得到的回报来评估$ \pi $ $$ \begin{aligned} G_t^{\pi/\mu}=\frac{\pi(A_t\mid S_t)}{\mu(A_t\mid S_t)}\frac{\pi(A_{t+1}\mid S_{t+1})}{\mu(A_{t+1}\mid S_{t+1})}\ldots\frac{\pi(A_T\mid S_T)}{\mu(A_T\mid S_T)}G_t\\ V(S_t)\leftarrow V(S_t)+\alpha\left(G_t^{\pi/\mu}-V(S_t)\right) \end{aligned} $$
- 缺点:方差过大;如果$ \mu $为 0 该方法失效
离策略 TD 学习
- 基于重要性采样,给 TD 目标添加权重,即$ R+\gamma V(S^\prime) $ $$ V(S_{t}) \leftarrow V(S_{t})+ \alpha\left(\frac{\pi(A_{t}\mid S_{t})}{\mu(A_{t}\mid S_{t})}\left(R_{t+1}+\gamma V(S_{t+1})\right)-V(S_{t})\right) $$
Q-Learning(SARSAMAX)
考虑动作值函数$ Q(s,a) $,不需要重要性采样
行为策略$ \mu $
- 实际选择动作的策略,即$ A_{t+1}\sim \mu(\cdot\mid S_t) $
- 在当前状态下,下一步动作从行为策略采样
- $ \epsilon $-贪婪策略
目标策略$ \pi $
用于更新值函数的策略,即$ A_{t}^{\prime}\sim \pi(\cdot\mid S_{t+1}) $
在下一状态中,从目标策略采样动作
$$ Q(S_t,A_t)\leftarrow Q(S_t,A_t)+\alpha\left({\color{red} R_{t+1}+\gamma Q(S_{t+1},A^{\prime})} -Q(S_t,A_t)\right) $$贪婪策略:$ \pi(S_{t+1})=\arg\displaystyle\max_{a^{\prime}}Q(S_{t+1},a^{\prime}) $
故有
$$ \begin{aligned} & R_{t+1}+\gamma Q(S_{t+1},A^{\prime}) \\ & =R_{t+1}+\gamma Q(S_{t+1},\arg\displaystyle\max_{a^{\prime}}Q(S_{t+1},a^{\prime})) \\ & =R_{t+1}+\displaystyle\max_{a^{\prime}}\gamma Q(S_{t+1},a^{\prime}) \end{aligned} $$
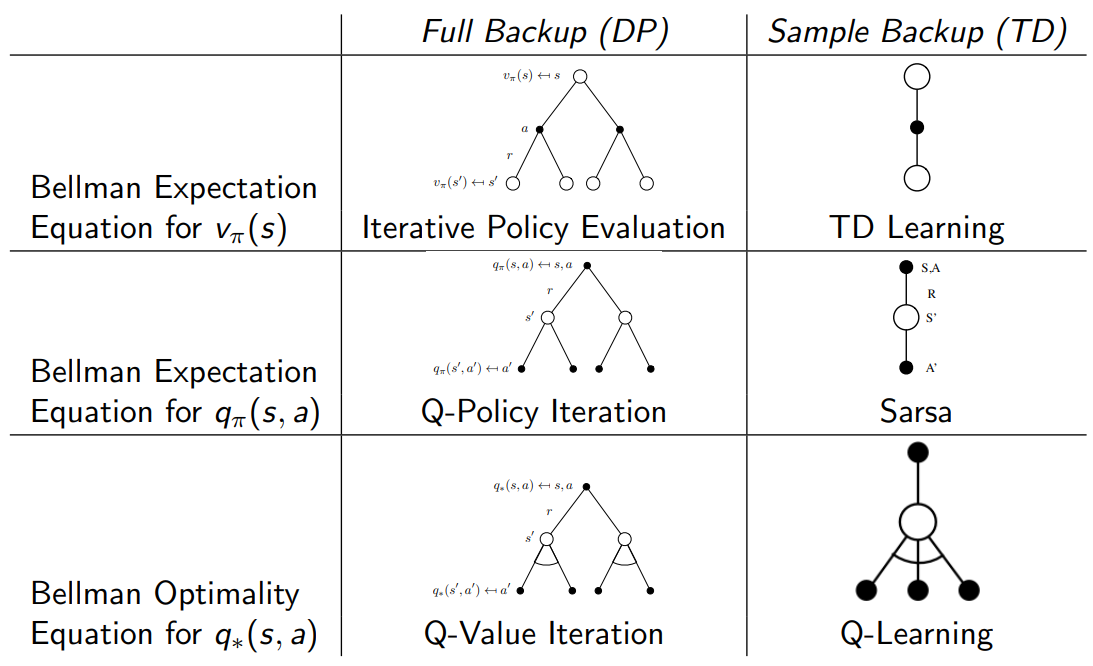
类别 Full Backup (DP) Sample Backup (TD) Bellman 期望方程($ v_\pi(s) $) Iterative Policy Evaluation
$ V(s) \leftarrow \mathbb{E}[R + \gamma V(S^{\prime}) \mid s] $TD Learning
$ V(S) \stackrel{\alpha}{\leftarrow} R + \gamma V(S^{\prime}) $Bellman 期望方程($ q_\pi(s, a) $) Q-Policy Iteration
$ Q(s, a) \leftarrow \mathbb{E}[R + \gamma Q(S^{\prime}, A^{\prime}) \mid s, a] $SARSA
$ Q(S, A) \stackrel{\alpha}{\leftarrow} R + \gamma Q(S^{\prime}, A^{\prime}) $Bellman 最优方程($ q_*(s, a) $) Q-Value Iteration
$ Q(s, a) \leftarrow \mathbb{E} \left[ R + \gamma \displaystyle\max_{a^{\prime} \in A} Q(S^{\prime}, a^{\prime}) \mid s, a \right] $Q-Learning
$ Q(S, A) \stackrel{\alpha}{\leftarrow} R + \gamma \displaystyle\max_{a^{\prime} \in A} Q(S^{\prime}, a^{\prime}) $
.png!blogimg)
.png!blogimg)