三、深度强化学习

3.1 值函数方法（DQN）

3.2 Actor-Critic（AC、A3C）

3.3 信赖域方法（TRPO、PPO）

3.3.1 信赖域方法

  • 相较于基于梯度的策略优化算法（如 REINFORCE、Actor-Critic），信赖域方法（Trust Region Methods）在优化策略时，限制新旧策略的差异以确保学习稳定性

  • Trust Region Policy Optimization（TRPO）

    • 基于 KL 散度约束的新旧策略差异，进行更新
    • 保证每次更新策略不会偏离当前策略太远

  • Proximal Policy Optimization（PPO）

    • 用裁剪目标函数（Clipped Objective）替代严格的 KL 散度约束
    • 简化实现，计算效率更高，常用于实际应用

  • TRPO 算法原理

    • 核心思想

      • 在优化策略时，采用信赖域的概念，确保更新后的新策略与旧策略之间的差异（通常用 KL 散度衡量）在一定范围内
      • 防止策略更新过快导致性能下降或失效

    • 策略优化目标：在策略$\pi_\theta$​ 的参数空间中最大化累计奖励的期望，即

      $$ \mathbb{E}_{s \sim \rho^\pi, a \sim \pi_\theta} [r(s, a)] $$
    • 信赖域约束 $$ \begin{aligned} \text{max}_{\theta} &\quad \mathbb{E}_{s \sim \rho^\pi} \left[ \frac{\pi_\theta(a\mid s)}{\pi_{\theta_{\text{old}}}(a\mid s)} A^{\pi_{\theta_{\text{old}}}}(s, a) \right]\\ \text{subject to} &\quad \mathbb{E}_{s \sim \rho^\pi} \left[ D_{\text{KL}}(\pi_\theta(\cdot\mid s) \parallel \pi_{\theta_{\text{old}}}(\cdot\mid s)) \right] \leq \delta \end{aligned} $$
    • 优势函数 $$ A^{\pi_{\theta_{\text{old}}}}(s, a) = Q^{\pi_{\theta_{\text{old}}}}(s, a) - V^{\pi_{\theta_{\text{old}}}}(s) $$

    • 需要显式计算费舍尔信息矩阵和逆矩阵

    • 通过二次规划（Quadratic Programming, QP）解决优化问题，计算复杂度较高

3.3.1 损失函数

  • 传统的策略梯度算法存在的问题

    • 高方差：策略梯度估计存在较大的方差，导致学习过程不稳定
    • 更新过大：策略更新可能过于剧烈，导致策略迅速偏离最佳策略，从而降低学习效果

  • PPO 的目标是最大化累积奖励，同时限制策略更新的幅度，防止过大的更新导致训练不稳定

  • 为此，PPO 采用裁剪策略（Clipped Objective）设计损失函数，具体包含以下两部分：

    • a. 策略损失（Policy Loss）：通过对比新旧策略的比率 $r_t$ 和优势函数 $A_t$ 计算：

      • 利用重要性采样（importance sampling）来估计在当前策略下的回报

        • 新旧策略比率：$rt(\theta) = \frac{\pi{\theta}(at \mid s_t)}{\pi{\text{old}}(at \mid s_t)}$，其中 $\pi{\theta}$ 是当前策略，$\pi_{\text{old}}$ 是旧策略

        • 可以使用对数计算：$rt(\theta) = \exp(\log \pi\theta(at \mid s_t) - \log \pi{\text{old}}(a_t \mid s_t))$

        • 无截断损失项$\mathcal{L}(\theta) = r_t(\theta) \cdot \text{A}_t$

      • 裁剪策略（Clipped Objective）：限制策略更新的幅度来保证训练稳定性，具体形式为：

        $$ \mathcal{L}_{\text{clip}}(\theta) = \mathbb{E}_t \left[ \min \left( r_t(\theta) A_t, \text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon) A_t \right) \right] $$

        其中：

        • $\epsilon$ 是一个超参数，通常取 0.1 到 0.2，用于控制裁剪范围。
        • $\text{clip}(r_t, 1-\epsilon, 1+\epsilon)$ 限制了策略比率的变化幅度，确保新策略不会偏离旧策略太远。
        • 通过取最小值，算法在优势函数为正或负的情况下都能防止过度优化。

      • 通常来说，策略损失计算公式为

        $$ \mathcal{L}_{\text{PG}}(\theta) = - \min \left( \mathcal{L}(\theta), \mathcal{L}_{clip}(\theta) \right) $$

    • b. 值函数损失（Value Function Loss）：值函数的损失通过最小化预测值 $V_{\phi}(s_t)$ 与实际折扣回报 $\hat{R}_t$ 之间的误差来优化：

      $$ \mathcal{L}_{\text{value}}(\phi) = \mathbb{E}_t \left[ \left( V_{\phi}(s_t) - \hat{R}_t \right)^2 \right] $$
      • 同样也可以通过裁剪策略计算值函数损失

    • c. 总损失函数：PPO 的总损失函数包括策略损失、值函数损失和熵奖励（用于增加探索）：

      $$ \mathcal{L}_{\text{PPO}}(\theta, \phi) = \mathcal{L}_{\text{PG}}(\theta) - c_1 \mathcal{L}_{\text{value}}(\phi) + c_2 \mathcal{H}(\pi_{\theta}) $$
      • $c_1$ 和 $c_2$ 是权重系数，用于平衡各个损失项
      • $\mathcal{H}(\pi_{\theta})$​ 是策略的熵，鼓励策略的多样性，从而促进探索

    • d. KL 惩罚项：在损失函数中加入一个 KL 惩罚项，用来监控新旧策略的 KL 散度：

      $$ L^{\text{KL}} = \mathbb{E} \left[ L^{\text{CLIP}}(\theta) - \beta D_{\text{KL}}(\pi_{\theta_{\text{old}}} \\mid \pi_{\theta}) \right] $$
      • 其中$\beta$是 KL 散度的惩罚系数
3.3.2 具体步骤

  • 采集数据

    • 使用当前策略 $\pi{\theta}$ 与环境交互，采集一批轨迹数据，包括状态 $s_t$、动作 $a_t$、奖励 $r_t$、下一状态 $s{t+1}$
    • 记录旧策略的概率分布 $\pi_{\text{old}}(a_t\mid s_t)$

  • 计算奖励和优势函数

    • 计算折扣累计回报 $R_t$（未来奖励的总和）
    • 计算优势函数 $A_t$

  • 更新网络参数

    • 更新策略网络：计算策略比率$rt(\theta)$和裁剪后的策略损失$\mathcal{L}{\text{PG}}(\theta)$
    • 更新值函数网络：使用均方误差损失$\mathcal{L}_{\text{value}}(\phi)$最小化值函数预测 $V_{\phi}(s_t)$ 和折扣回报 $\hat{R}_t$ 之间的差异
    • 总损失函数：总损失函数$\mathcal{L}_{\text{PPO}}(\theta, \phi)$结合策略损失、值函数损失和熵正则项

  • 执行梯度更新：使用优化器对策略网络参数 $\theta$ 和值函数网络参数 $\phi$ 执行梯度下降更新：

    $$ \begin{aligned} \theta \leftarrow \theta - \eta \nabla_{\theta} \mathcal{L}_{\text{PPO}}(\theta, \phi)\\ \phi \leftarrow \phi - \eta \nabla_{\phi} \mathcal{L}_{\text{PPO}}(\theta, \phi) \end{aligned} $$
3.3.3 RLOO
  • 与 POO 的区别
    • RLOO 将 整个模型补全 视为单一动作，而常规 PPO 将 每个补全 token 视为单独的动作
    • 在 PPO 中，只有 EOS token 获得真正的奖励，奖励非常稀疏
    • 常规 PPO 会将奖励归因于 EOS token，而 RLOO 会将 EOS 奖励归因于整个补全
3.3.4 组相对策略优化（GRPO）

  • 在 LLM 环境中，奖励模型通常只为最后一个标记分配奖励分数，这可能会使训练针对每个标记都准确的价值函数变得复杂

    PPO vs GRPO

  • GRPO 目标函数：

    $$ \mathcal{J}_{\mathrm{GRPO}}(\theta)=\mathbb{E}\left[q\sim P(Q),\{o_i\}_{i=1}^G\sim\pi_{\theta_{ad}}(O\mid q)\right]\left[\frac{1}{G}\sum_{i=1}^G\frac{1}{\mid o_i\mid }\sum_{t=1}^{\mid o_i\mid }\left\{\min\left[\frac{\pi_\theta(o_{i,t}\mid q,o_{i,\lt t})}{\pi_{\theta_{ad}}(o_{i,t}\mid q,o_{i,\lt t})}\hat{A}_{i,t},\operatorname{clip}\left(\frac{\pi_\theta(o_{i,t}\mid q,o_{i,\lt t})}{\pi_{\theta_{ad}}(o_{i,t}\mid q,o_{i,\lt t})},1-\epsilon,1+\epsilon\right)\hat{A}_{i,t}\right]-\beta D_{KL}\left[\pi_\theta\parallel\pi_{\mathrm{ref}}\right]\right\}\right] $$

  • KL 散度的无偏估计：

    $$ \mathrm{D}_{KL}\left[\pi_{\theta}\mid \mid \pi_{ref}\right]=\frac{\pi_{ref}(o_{i,t}\mid q,o_{i,\lt t})}{\pi_{\theta}(o_{i,t}\mid q,o_{i,\lt t})}-\log\frac{\pi_{ref}(o_{i,t}\mid q,o_{i,\lt t})}{\pi_{\theta}(o_{i,t}\mid q,o_{i,\lt t})}-1 $$

  • 优势函数：

    $$ \hat{A}_{i,t}=\widetilde{r_{i}}=\frac{r_{i}-\mathrm{mean}(\mathbf{r})}{\mathrm{std}(\mathbf{r})} $$

四、强化学习与大语言模型

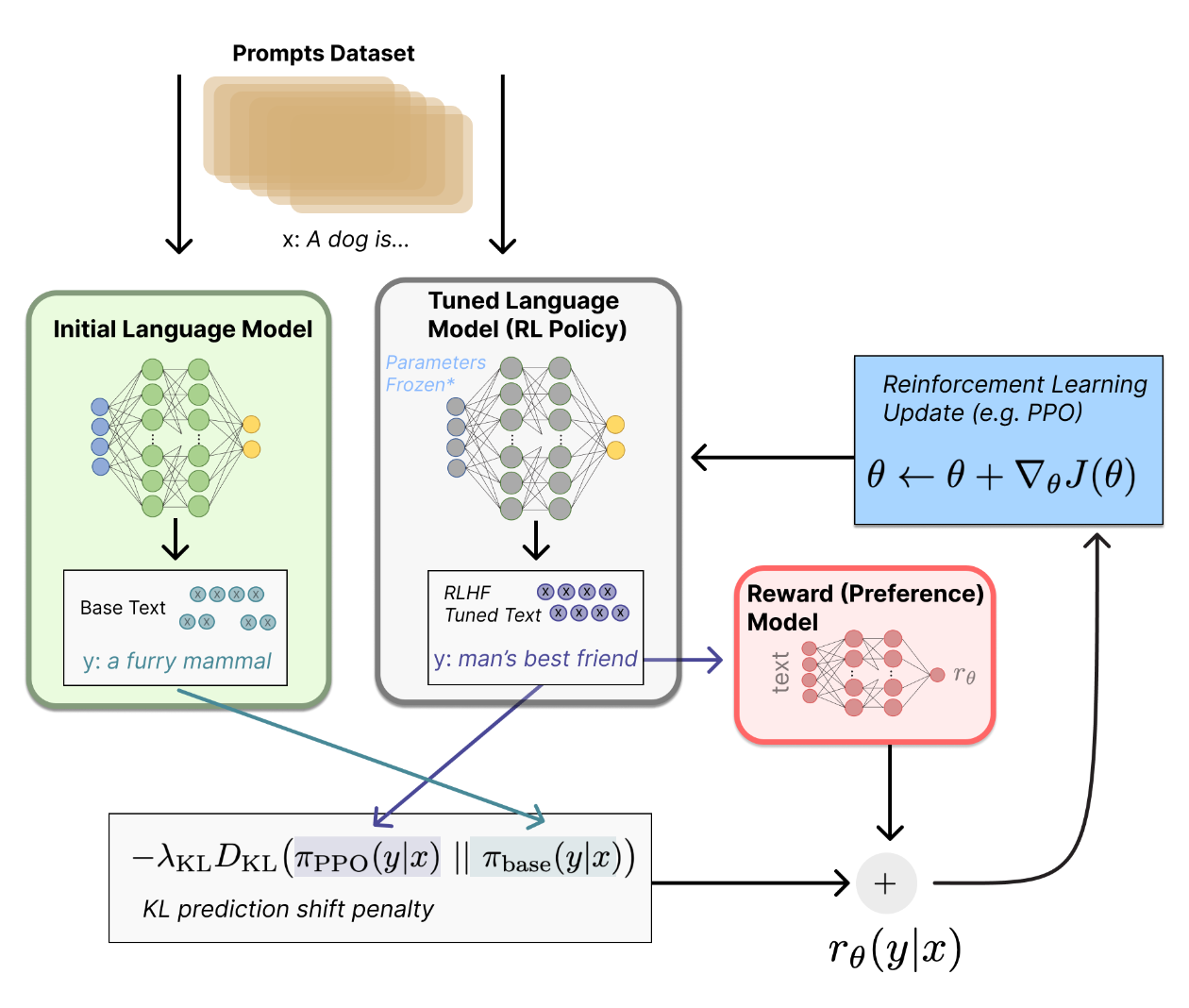
4.1 RLHF 范式

  • RLHF 的流程

    • SFT 监督微调阶段：得到$\pi^{SFT}$

    • 奖励建模阶段

      • 根据 Bradley-Terry（BT）模型，偏好分布$p^{\star}$可以建模为

        $$ p^*(y_1\succ y_2\mid x)=\frac{\exp\left(r^*(x,y_1)\right)}{\exp\left(r^*(x,y_1)\right)+\exp\left(r^*(x,y_2)\right)} $$

      • 假设从偏好分布$p^{\star}$采样得到数据集（人类偏好反馈数据集）$\mathcal{D}={x^{(i)},yw^{(i)},y_l^{(i)}}^N{i=1}$

      • 可以通过最大似然估计奖励模型$r_\phi(x,y)$的参数

        $$ \mathcal{L}_{R}(r_{\phi},\mathcal{D})=-\mathbb{E}_{(x,y_{w},y_{l})\sim\mathcal{D}}\left[\log\sigma(r_{\phi}(x,y_{w})-r_{\phi}(x,y_{l}))\right] $$

      • 通常，奖励模型从$\pi^{SFT}$初始化，并在最后加一层线性层来生成标量奖励

      • 为了降低方差，可以正则化奖励，如

        $$ ​ \mathbb{E}_{x,y\sim\mathcal{D}}\left[r_{\phi}(x,y)\right] $$

      奖励模型建模

    • 强化学习阶段

      • 利用奖励模型为 LLM 提供反馈，目标为最大化奖励，建模为

        $$ \max_{\pi_{\theta}}\mathbb{E}_{x\sim\mathcal{D},y\sim\pi_{\theta}(y\mid x)}\left[r_{\phi}(x,y)\right]-\beta\mathbb{D}_{\mathrm{KL}}\left[\pi_{\theta}(y\mid x)\parallel\pi_{\mathrm{ref}}(y\mid x)\right] $$

      • $\beta$用于控制策略模型和参考模型之间的偏差

      • 策略模型和参考模型均使用$\pi^{SFT}$初始化

      • 由于该目标不可微分，可以通过以下奖励函数建模

        $$ r(x,y)=r_{\phi}(x,y)-\beta(\log\pi_{\theta}(y\mid x)-\log\pi_{\mathrm{ref}}(y\mid x)) $$

​ 强化学习阶段

4.2 直接偏好优化（DPO）

  • 直接偏好优化

    • 最大化奖励建模的最优解形式如下

      $$ \begin{align} \text{Objective Function}&=\max_{\pi_\theta}\mathbb{E}_{x\sim\mathcal{D},y\sim\pi_\theta(y\mid x)}\left[r_\phi(x,y)\right]-\beta\mathbb{D}_{KL}\left[\pi_\theta(y\mid x)\parallel\pi_{\mathrm{ref}}(y\mid x)\right] \\ & =\max_\pi\mathbb{E}_{x\sim\mathcal{D}}\mathbb{E}_{y\sim\pi(y\mid x)}\left[r(x,y)-\beta\log\frac{\pi(y\mid x)}{\pi_{\mathrm{ref}}(y\mid x)}\right] \\ & =\min_\pi\mathbb{E}_{x\sim\mathcal{D}}\mathbb{E}_{y\sim\pi(y\mid x)}\left[\log\frac{\pi(y\mid x)}{\pi_{\mathrm{ref}}(y\mid x)}-\frac{1}{\beta}r(x,y)\right] \\ & =\min_\pi\mathbb{E}_{x\sim\mathcal{D}}\mathbb{E}_{y\sim\pi(y\mid x)}\left[\log\frac{\pi(y\mid x)}{\frac{1}{Z(x)}\pi_{\mathrm{ref}}(y\mid x)\exp\left(\frac{1}{\beta}r(x,y)\right)}-\log Z(x)\right]\\ \pi_r(y\mid x)&=\frac{1}{Z(x)}\pi_{\mathrm{ref}}(y\mid x)\exp\left(\frac{1}{\beta}r(x,y)\right)\\ Z(x)&=\sum_{y}\pi_{\mathrm{ref}}(y\mid x)\exp\left(\frac{1}{\beta}r(x,y)\right) \end{align} $$
      • 其中$Z(x)$为配分函数

    • 对上式两边取对数，得到奖励函数（也即 BT 模型中的“能力”）

      $$ r(x,y)=\beta\log\frac{\pi_{r}(y\mid x)}{\pi_{\mathrm{ref}}(y\mid x)}+\beta\log Z(x) $$

    • 代入 BT 模型

      $$ \begin{aligned} p^{*}(y_{1}\succ y_{2}\mid x) & =\frac{\exp\left(\beta\log\frac{\pi^*(y_1\mid x)}{\pi_{\mathrm{ref}}(y_1\mid x)}+\beta\log Z(x)\right)}{\exp\left(\beta\log\frac{\pi^*(y_1\mid x)}{\pi_{\mathrm{ref}}(y_1\mid x)}+\beta\log Z(x)\right)+\exp\left(\beta\log\frac{\pi^*(y_2\mid x)}{\pi_{\mathrm{ref}}(y_2\mid x)}+\beta\log Z(x)\right)} \\ & =\frac{1}{1+\exp\left(\beta\log\frac{\pi^*(y_2\mid x)}{\pi_{\mathrm{ref}}(y_2\mid x)}-\beta\log\frac{\pi^*(y_1\mid x)}{\pi_{\mathrm{ref}}(y_1\mid x)}\right)} \\ & =\sigma\left(\beta\log\frac{\pi^*(y_1\mid x)}{\pi_{\mathrm{ref}}(y_1\mid x)}-\beta\log\frac{\pi^*(y_2\mid x)}{\pi_{\mathrm{ref}}(y_2\mid x)}\right)\\ &=\sigma\left(r(x,y_1)-r(x,y_2)\right) \end{aligned} $$

    • 制定最大似然目标

      $$ \begin{aligned} \mathcal{L}_R(r_\phi,\mathcal{D}) & =-\mathbb{E}_{(x,y_w,y_l)\sim\mathcal{D}}\left[\log\sigma\left(r_\phi(x,y_w)-r_\phi(x,y_l)\right)\right] \\ & =-\mathbb{E}_{(x,y_w,y_l)\sim\mathcal{D}}\left[\log\sigma\left(\beta\log\frac{\pi_\theta(y_w\mid x)}{\pi_{\mathrm{ref}}(y_w\mid x)}-\beta\log\frac{\pi_\theta(y_l\mid x)}{\pi_{\mathrm{ref}}(y_l\mid x)}\right)\right] \\ & =\mathcal{L}_{\mathrm{DPO}}(\pi_\theta;\pi_{\mathrm{ref}}) \end{aligned} $$

    • 分析该损失函数的梯度

      $$ \begin{aligned} \nabla_{\theta}\mathcal{L}_{\mathrm{DPO}}(\pi_{\theta};\pi_{\mathrm{ref}})&=-\mathbb{E}_{(x,y_{w},y_{l})\sim\mathcal{D}}\left[\frac{\sigma^{\prime}\left(u\right)}{\sigma\left(u\right)}\nabla_{\theta}\left(u\right)\right] \\ & = -\beta\mathbb{E}_{(x,y_{w},y_{l})\sim\mathcal{D}}\left[\underbrace{\sigma(\hat{r}_{\theta}(x,y_{l})-\hat{r}_{\theta}(x,y_{w}))}_{\text{higher weight when reward estimate is wrong}}\left[\underbrace{\nabla_{\theta}\log\pi(y_{w}\mid x)}_{\text{increase likelihood of }y_{w}}-\underbrace{\nabla_{\theta}\log\pi(y_{l}\mid x)}_{\text{decrease likelihood of }y_{l}}\right]\right]\\ u&=\beta\log\frac{\pi_\theta(y_l\mid x)}{\pi_\mathrm{ref}(y_l\mid x)}-\beta\log\frac{\pi_\theta(y_w\mid x)}{\pi_\mathrm{ref}(y_w\mid x)} \end{aligned} $$

    • 其中隐式奖励模型$\hat{r}_{\theta}(x,y)=\beta\log\frac{\pi_{\theta}(y\mid x)}{\pi_{\mathrm{ref}}(y\mid x)}$

    • 当真实参考分布不可用时，可以采用偏好对的最大似然估计：$\pi_{\mathrm{ref}}=\arg\max_\pi\mathbb{E}_{x,y_w\thicksim\mathcal{D}}\left[\log\pi(y_w\mid x)\right]$​

  • Bradley-Terry 模型

    • 建模成对比较数据的概率模型，通常用来预测多个对象之间的相对优劣（如排名、胜率等）

    • 假设有 $n$ 个对象 $A_1, A_2, \dots, A_n$，每个对象 $A_i$ 都有一个正的能力值（或评分） $\pi_i > 0$

      • Bradley-Terry 模型定义了两两比较中对象获胜的概率
      • 对于对象 $A_i$ 和 $A_j$：
      $$ P(A_i \text{ Defeat } A_j) = \frac{\pi_i}{\pi_i + \pi_j} $$
      • 其中 $\pi_i$ 和 $\pi_j$ 分别是 $A_i$ 和 $A_j$ 的能力值

    • 对于 $Ai$ 和 $A_j$，如果已知 $A_i$ 和 $A_j$ 比赛了 $n{ij}$ 次，且 $Ai$ 赢了 $w{ij}$ 次，则其获胜的概率可以用最大似然估计（MLE）求解，似然函数为：

      $$ L(\pi_1, \pi_2, \dots, \pi_n) = \prod_{i \lt j} \left( \frac{\pi_i}{\pi_i + \pi_j} \right)^{w_{ij}} \left( \frac{\pi_j}{\pi_i + \pi_j} \right)^{l_{ij}} $$
      • 其中 $l{ij} = n{ij} - w_{ij}$ 为 $A_j$ 胜利的次数

    • 对数似然函数：

      $$ \log L = \sum_{i \lt j} w_{ij} \log \pi_i - (w_{ij} + l_{ij}) \log (\pi_i + \pi_j) $$

  • Plackett-Luce 模型

    • 将 BT 模型推广至建模排序数据

    • 给定一组对象 ${A_1, A_2, \dots, A_n}$，Plackett-Luce 模型定义了以下排序概率：

      • 假设 $\sigma = (\sigma_1, \sigma_2, \dots, \sigma_n)$ 是对象的一个排序（即 $\sigma_1$ 是第 1 名，$\sigma_2$ 是第 2 名，依此类推），
      • 排序 $\sigma$ 的概率为： $$ P(\sigma) = \prod_{j=1}^n \frac{\pi_{\sigma_j}}{\sum_{k=j}^n \pi_{\sigma_k}}, $$
      • 其中，$\pi_{\sigma_j}$ 是对象 $\sigma_j$​ 的能力值，分母表示从剩余未排序对象中选择当前对象的概率

    • 最大似然估计（MLE）：给定观测到的排序数据 ${\sigma^{(1)}, \sigma^{(2)}, \dots, \sigma^{(m)}}$，

      • 似然函数为： $$ L(\pi_1, \pi_2, \dots, \pi_n) = \prod_{i=1}^m P(\sigma^{(i)}), $$
      • 对似然函数取对数后，通过优化算法（如梯度下降）求解

五、问题思考

5.1 强化学习亟待解决的问题

  • 样本效率低下
    • 语言和视觉任务涉及庞大而复杂的状态-动作空间，这使得强化学习智能体难以学习有效的策略
    • 智能体必须理解任务并将其与相应的状态联系起来，这需要更广泛的交互
  • 奖励函数设计
    • 在语言和视觉任务中，设计有效的奖励函数尤其具有挑战性。这些函数必须捕捉微妙的语言细微差别和复杂的视觉特征，这大大增加了本已困难的过程的复杂性。
    • 在这些领域中，将奖励与高级任务目标相结合通常需要领域专业知识和大量的反复试验
  • 泛化
    • 强化学习代理通常会过度拟合训练数据，尤其是在基于视觉的环境中，导致在有干预（例如添加噪音）的状态下部署时性能不佳。代理必须学习对此类干预具有鲁棒性的不变特征，从而能够在不同的语言环境和视觉场景中实现泛化。 然而，这些领域的复杂性使得提取此类特征并适应新环境特别具有挑战性
  • 自然语言理解
    • 深度强化学习在自然语言处理和理解场景中面临困难，其中人类语言的细微差别和复杂性带来了独特的挑战，而当前的强化学习方法无法充分解决这些挑战
  • 奖励黑客（Reward Hacking）
    • 当强化学习（RL）代理利用奖励函数中的缺陷或模糊性来获得高额奖励，而没有真正学习或完成预期任务时，奖励黑客就会发生
    • 奖励黑客行为的存在是因为强化学习环境通常不完美，并且准确设计奖励函数从根本上来说是一项重大挑战
    • 解决方法
      • 动态调整奖励函数：通过持续监控智能体行为，动态更新奖励函数，防止固定奖励机制被智能体利用
      • 引入对抗训练：训练额外的判别器或模型检测奖励黑客行为，限制智能体对奖励函数漏洞的利用
      • 多层次奖励建模：将 PRM 与结果奖励模型结合，通过最终目标奖励约束中间奖励优化，防止中间步骤过拟合

  • 奖励稀疏（Reward Sparsity）

    • 智能体在环境中执行动作后，很少或者根本得不到有意义的奖励信号
    • 奖励信号的缺乏使得学习过程变得非常困难，因为强化学习算法需要通过奖励信号来引导策略的改进
    • 使用过程奖励模型 PRM 可以提供更密集的奖励信号，能够指导长程任务的中间优化

  • 语言模型的应用已从语言建模转向任务解决，从基本的文本分类和情感分析到复杂的高级任务规划和决策

5.2 LLM 代理亟待解决的问题

  • 上下文长度有限
    • 上下文容量有限，限制了包含历史信息、详细说明、API 调用上下文和响应
    • 系统的设计必须适应这种有限的通信带宽，而从过去的错误中学习的自我反思等机制将从长或无限的上下文窗口中受益匪浅
    • 尽管向量存储和检索可以提供对更大知识池的访问，但它们的表示能力不如全注意力机制那么强大
  • 长期规划和任务分解的挑战
    • 长期规划和有效探索解决方案空间仍然具有挑战性。 LLMs 当遇到意外错误时，很难调整计划，这使得它们与从试错中学习的人相比不太稳健
  • 自然语言接口的可靠性
    • 当前的代理系统依赖自然语言作为 LLMs 与外部组件（例如内存和工具）之间的接口。
    • 然而，模型输出的可靠性值得怀疑，因为 LLMs 可能会出现格式错误，并且偶尔会表现出叛逆行为（例如拒绝遵循指令）
    • 因此，大部分论文中的工作都专注于解析模型输出

学习资源